
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
*주의*
온라인 강의를 들으면서 정리한 내용이라, 틀린 부분과 대충 넘어간 부분이 많을 수 있습니다.
Node Embedding

기존의 Graph를 딥러닝에서 다루기 위해서는 Graph를 구조화된 데이터 형태에 맞춰야할 필요가 있었다.
하지만, 이제는 그래프를 자동으로 벡터 형태로 만들어 낼 수 있기 때문에 효율적인 딥러닝이 가능해 졌다.

예를 들어 DeepWalk에서는 input 그래프를 다음과 같이 2차원을 표현해 냈다.

이와 같은 과정을 node embedding이라고 한다.
임베딩이란 사람이 쓰는 자연어를 기계가 이해할 수 있는 벡터 형태로 바꾸는 과정을 의미한다.
https://casa-de-feel.tistory.com/28
임베딩(Embedding)이 뭐지?
*해당 포스팅은 한국어 임베딩(이기창 지음)을 공부하며 작성한 글입니다. 안녕하세요! 오늘은 자연어 처리 분야의 임베딩의 기초적인 부분에 대해 알아보겠습니다. 임베딩을 공부하게 된 계기
casa-de-feel.tistory.com

실제 그래프에서 연관이 있는 노드라면, 임베딩 차원에서는 내적과 같은 계산으로 연관성을 구할 수 있다.

내적은 한 벡터로의 그림자 같이 표현할 수 있는데, 연관성이 높을 수록 비슷한 방향성의 벡터가 될 것이고, 비슷할 수록 내적값이 높게 계산된다.
전혀 연관이 없다면 두 벡터는 90도로 직교할 것이고, 내적은 0이 된다.
그렇다면 node u를 embedding한 encode(u) = Z(u)는 어떻게 구할까?
이때 사용하는 것이 embedding-lookup이다.
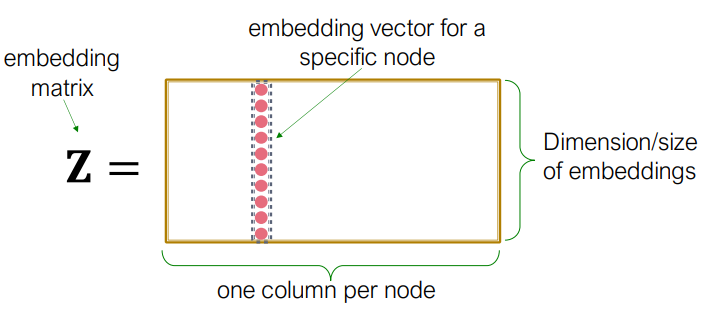
embedding matrix Z는 각 node당 column을 가진다.
따라서 Graph의 크기가 클 수록 파라미터 양이 증가해 계산이 느려질 수 밖에 없다.
Random Walks
일단 노드 간의 유사성을 확인하기 위한 random walk에 대해 알아보자.
여기서는 노드의 라벨링과 데이터는 사용하지 않을 것이다.
node u가 embedding 된 vector를 Z(u)라고 하자.
이때 node u에서 random walk를 시작해 node v를 방문할 가능성은 P(v | Z(u))이다.
사용할 수 있는 비선형 함수로는 SoftMax 혹은 Sigmoid가 있다.
Random Walks에서는 시작 노드로 부터 random하게 이웃 노드를 방문한다.

이와 같은 과정을 수많이 반복하면 u에서 v로 도달 할 수 있는 가능성을 구할 수 있다. => P(v|u)
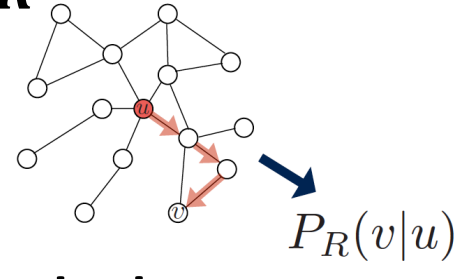
이러한 과정에서 이웃 노드, 서로에게 간선이 많은 노드일 수록 방문 확률이 높다.
따라서 embedding된 Z(v)와 Z(u)간의 유사도는 P(v|u)에 가깝도록 만들어야 한다.
또한 v,u 간의 유사도가 높고 u,k 간의 유사도도 높다면 v,k간의 유사도도 높을 것으로 추정할 수도 있어, 효율적이다.
이제 Random walks를 진행해보자.

1. 시작인 node u에서 고정된 길이 만큼의 random walks를 시작한다.
2. u의 이웃인 neighbors(u)들(u에서 random walks로 도달가능한 노드들)에 대해 likelihood를 최대화 시키는 Z(u)를 찾아가자.
likelihood는 간단히 하면 데이터가 어떤 곡선에서 추출 되었을 가능성이 높은지를 판단한는 것이다.

예를 들어 위의 1,4,5,6,9 데이터는 주황색 곡선에서 추출 되었을 가능성이 높다고 볼 수 있다.
이때 softMax를 이용하면, 그래프 상의 모든 노드 n에 대해 u의 이웃인 v의 확률은 다음과 같다.


이제 L을 최소화하는 Z(u)를 찾아내면 된다.
하지만, 모든 메트릭스의 정점에 대해 계산하면 O(|V^2|)의 복잡도가 소요된다.
이를 최적화 하기위해 Negative Sampling으로 근사 값을 이용하는 방법을 사용한다.'
Negative Sampling의 예시는 다음 게시글을 참조하자.
https://sulung-sulung.tistory.com/38
Negative sampling 이란?
Word2Vec 모델에서 negative sampling 이란? 단어뭉치(corpus)의 개수가 1000 개 이고 hidden layer크기가 3000이라 하면, W와 , W`의 크기는 1000x3000 이다. Input vector는 one-hot 벡터로 1숫자만 1이고 나머진 모두 0이
sulung-sulung.tistory.com
정리하자면, 서로에게 영향이 큰 노드에 비해, 영향이 적은 노드의 수가 훨씬 많기 때문에 영향이 적은 모든 노드를 확인해볼 필요는 없다.

이때의 K는 robust한 값을 사용하는데, 보통 5~20 사이이다.
우리는 다음과 같은 Object Function을 얻었으므로, 경사 하강법을 통해 최적화해 나가자.

이를 위해 L을 Z로 미분해야 한다.
모든 것을 고려하는 것보다는 SGD를 통해 mini-batch를 사용해 미분하는 것이 효율적이다.
하지만 이러한 방식은 각 노드에서 고정된 길이의 Random walks만 진행하는 것으로 제약이 너무 많다.
이를 해결한 것이 node2vec이다.
Node2Vec
다음 노드를 선택하는 방식은 BFS 혹은 DFS가 있다.

BFS는 근처 노드만 방문하는 대신 지역의 전체적인 구조를 파악할 수 있다.
DFS는 깊이 탐색하므로 전체적인 구조를 파악할 수 있지만, 지역적인 구조는 파악할 수 없다.

결국 두 탐색은 trade-off 관계를 가진다. 따라서 둘을 적절히 이용해야 한다.
node2vec은 이러한 탐색 전략으로 node embedding에 더 풍부한 정보를 인코딩 한다.
S1 노드에서 W로 진행한 상황에서는 3가지 선택지가 있다.

다시 S1으로 복귀(return), S1->W과 같은 거리의 S2로 이동(BFS), 더 깊은 S3로 이동(DFS)

고정된 수 만큼 random walk를 진행하는 것은 동일 하지만, 여러 탐색 전략을 사용하여 반복하는 것이 node2vec이다.
여러가지 Embedding 방식
전체 그래프를 embedding 하는 방법에는 3가지가 있다.

1. 임베딩된 매트릭스 Z를 각 node의 column vector들의 sum으로 나타낸다.
2. 가상의 노드를 만들어서 임베드 공간에서 서브 그래프를 표현하도록 한다.

3. Anonymous Walk Embeddings

Random Walk1과 2에 방문한 순서대로 index를 붙이면, 결국 같은 Anonymous Walk가 된다.
다음은 Anonymous Walk의 길이에 따라, 나올 수 있는 탐색 경우의 수이다.

예를 들어 길이가 3인 Anonymous Walk는 1에서 시작할 때, 다음과 같이 5개의 path를 가질 수 있다.
1 -> 1 -> 1
1 -> 1 -> 2 (두번째 다른 노드)
1 -> 2 -> 1
1 -> 2 -> 2
1 -> 2 -> 3 (3번째 다른 노드)
이렇게 생성되는 Anonymous Walk의 path 별로 각 노드의 column 벡터의 값으로 적용하면
길이가 3인 Anonymous Walk에서는 5차원 vector가 된다.
각 원소 Wi,j 의 값은 i에서 시작하는 Anonymous Walk에서 해당 path(j)가 등장하는 빈도수로 볼 수 있다.
Anonymous Walk 방식으로 Sampling 데이터를 만들기 위해서는 독립적으로 m번의 random walk가 진행되어야 한다.

길이가 7인 Anonymous Walk는 총 877 가지의 path가 나온다.
이때 각 path별 빈도수를 전부 채우려면, 모든 노드를 출발 노드로 선택하고, 각각 122,500번의 random walk를 실행해야 한다.
이 또한 너무 많은 계산이 필요하다.
따라서 빈도수를 예측하는 모델이 연구되었다. window size = k를 설정하고
path 중에 하나인, W(j)를 구하기 위해 W(j-k), W(j - (k+1)), .... , W(j - 1)를 이용하는 방식이다.

이러한 3가지 방식으로 만든 node embedding matrix Z로 node간의 내적을 통한 연관성을 구해, 노드간의 분류도 가능해진다.
이외에도 계층을 통한 embedding 방식도 있다.

참조
강의 자료: http://web.stanford.edu/class/cs224w/index.html
강의 영상: https://www.youtube.com/watch?v=JAB_plj2rbA&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn
참조 게시글: https://velog.io/@tobigsgnn1415/Node-Embeddings
'CS > GNN' 카테고리의 다른 글
| Attention 간단 정리 (0) | 2023.02.23 |
|---|---|
| Seq2Seq 간단 정리 (0) | 2023.02.23 |
| [논문 리뷰] LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation (0) | 2023.01.05 |
| [GNN] Graph Neural Network - 2 (0) | 2023.01.04 |
| [GNN] Graph Neural Networks - 1 (0) | 2023.01.03 |