
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://www.acmicpc.net/problem/2533
2533번: 사회망 서비스(SNS)
첫 번째 줄에는 친구 관계 트리의 정점 개수 N이 주어진다. 단, 2 <= N <= 1,000,000이며, 각 정점은 1부터 N까지 일련번호로 표현된다. 두 번째 줄부터 N-1개의 줄에는 각 줄마다 친구 관계 트리의 에지
www.acmicpc.net
풀이
solved.ac 난이도: Gold 3
트리에서 다이나믹 프로그래밍을 적용하는 문제.
다행히 얼리 어뎁터들에 의해 정보가 확산되어 다른 얼리 어뎁터들이 다시 정보를 확산시키는 것이 아닌 초기의 상태만을 확인한다.
해당 노드가 얼리 어뎁터가 되기 위해서는 자신의 주변 노드(부모와 자식 노드들)가 얼리 어뎁터여야 한다.
따라서 모든 트리의 노드들이 얼리 어뎁터가 되기 위해서는 다음과 같은 경우들이 존재한다.
자신이 얼리 어뎁터라면 두 가지 경우로 분기할 수 있다. (부모는 얼리 어뎁터일 수 도 있고 아닐 수도 있다.)
1. 자식 노드가 얼리 어뎁터인 경우
2. 자식 노드가 얼리 어뎁터가 아닌 경우
하지만 자신이 얼리 어뎁터가 아니라면
부모는 항상 얼리 어뎁터이고 자식 노드들도 반드시 얼리 어뎁터여야 한다.
여기서 자신이 얼리 어뎁터라면 자식들이 항상 얼리 어뎁터가 아닌 게 최솟값이 나오지 않을까 생각할 수 있지만 아래와 같은 경우를 생각해보자.

u의 자식 노드 v는 얼리 어뎁터인 것이 v의 많은 자식 노드들을 한 번에 얼리 어뎁터로 만들 수 있어 더 효율적이다.
만약 u의 자식 노드를 모두 얼리 어뎁터를 아니게 만든다면 v노드 만을 위해 v의 자식 노드들이 모두 얼리 어뎁터가 되어야 한다.
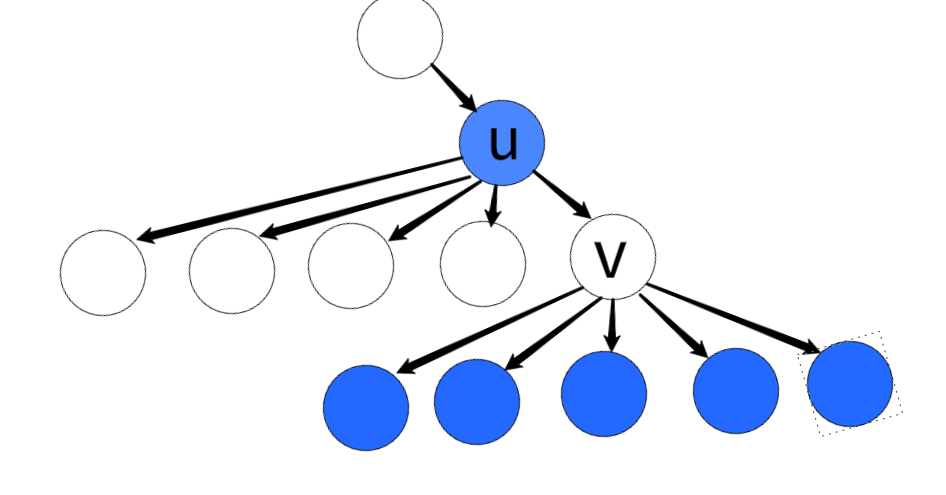
따라서 현재 노드를 루트 노드로 하는 서브 트리 들의 각각의 최소 얼리 어뎁터 수를 구해주자.
이를 구하기 위해 자식 노드가 얼리 어뎁터인 경우의 서브 트리에서의 최솟값과
얼리 어뎁터가 아닌 경우의 최솟값을 구하여 비교해 준 후 더 작은 값을 사용하자.
또한 최소의 어뎁터만 색칠된 트리를 생각해보자.
이때 굳이 노드 1이 루트가 아니어도 어떤 노드를 루트로 선택하든 노드들의 주변 노드들은 변하지 않는다.
결국 어떤 노드가 부모가 되고 자식이 되든 주변 노드가 모두 얼리 어뎁터여야 하는 것은 변하지 않는다.
따라서 결과에는 영향을 미치지 않는다.
이를 구현하기 위해 Node클래스를 작성하였다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
int node_num;
int dp[1000001][2];
class Node; // 클래스 선언부
vector<Node> tree;
class Node{ //클래스 정의부
public:
int parent;
vector<int> children;
void FindParentDFS(int par, int now){
parent = par;
for(int i=0; i<children.size() ; ++i)
if(children[i] != parent)
tree[children[i]].FindParentDFS(now,children[i]);
}
int MinEarlyAdaptor(int node, int is_adaptor){
int& ret = dp[node][is_adaptor];
if(ret != -1)
return ret;
int min_result=0;
ret =0;
for(int i=0; i<children.size() ; ++i){
if(children[i] != parent){
min_result = tree[children[i]].MinEarlyAdaptor(children[i], 1);
if(is_adaptor) //node가 어뎁터인 경우
min_result = min(min_result, tree[children[i]].MinEarlyAdaptor(children[i], 0));
ret += min_result;
}
}
if(is_adaptor) //자기 자신이 어뎁터인 경우 +1
++ret;
return ret;
}
};
|
cs |
MinEarlyAdaptor() 는 현재 노드(node)가 얼리 어뎁터 인지의 여부(is_adaptor)를 사용하여 자식 노드들을 방문한다.
is_adaptor가 1인 경우(현재 노드가 얼리 어뎁터인 경우)만 자식 노드들을 어뎁터가 아니도록 만들 수 있음을 주의하자.
다이나믹 프로그래밍을 사용하였기 때문에 각 노드들은 어뎁터인 경우와 아닌 경우, 각각 두 번씩만 방문하면 된다.
따라서 시간 복잡도는 O(N)이 소모되어 시간 안에 충분히 해결 가능하다.
코드
'알고리즘 공부 > 백준' 카테고리의 다른 글
| [백준] No.1693 - 트리 색칠하기 (C++) (379) | 2021.02.13 |
|---|---|
| [백준] No.1289 - 트리의 가중치 (C++, 트리) (0) | 2021.02.11 |
| [백준] No.3176 - 도로 네트워크 (C++, 최소 공통 조상) (0) | 2021.02.07 |
| [백준] No.1761 - 정점들의 거리 (C++, 최소 공통 조상) (0) | 2021.02.07 |
| [백준] No.11438 - LCA 2 (C++, 최소 공통 조상) (2) | 2021.02.06 |