
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
[Fenwick Tree Lazy propagation] - 펜윅 트리에 Lazy propagation 적용하기
EVEerNew 2021. 2. 27. 15:16Fenwick Tree 펜윅 트리
기존의 펜윅 트리에 대해서는 깔끔하게 설명하신 백준님의 게시글을 보고 오자.
펜윅 트리 (바이너리 인덱스 트리) - BaekJoon
펜윅 트리는 세그먼트 트리와는 다르게 부분 합(첫 원소에서 부터 i개의 값)을 계산하는데 특화되었다.(이 특징이 가장 중요합니다!!!)
백준 님이 설명한 펜윅 트리에서는 점 업데이트(Point Update)와 구간 쿼리(Range query)가 가능하다.
따라서 [L,R]구간의 구간합은 [1,R]까지의 합(pSum(R) ) - [1,L-1]까지의 합( pSum(L-1) )으로 구할 수 있다.
하지만 원소의 업데이트는 한 개씩만 진행할 수 있다.
따라서 백준 - 수열과 쿼리 21(16975) 문제와 같은 구간의 업데이트를 요구하는 문제는 일일이 원소를 업데이트할 경우 구간 업데이트마다 O(NlogN)의 복잡도가 소요되므로 시간 안에 해결할 수 없다.
위의 문제를 해결하기 위해 펜윅 트리의 원소들을 다르게 나타낸다면
구간 업데이트(Range Update)와 점 쿼리(Point query)가 가능한 펜윅트리를 만들 수 있다.
문제에서 처리하는 두 가지 질의 아래와 같다.
Query 1: Ai, Ai+1, ..., Aj에 k를 더한다
Query 2: Ax 를 출력한다.
길이가 N인 수열 A를 다음과 같이 표현해보자.
B[1] = A[1], B[i] = A[i] - A[i-1]
1번 쿼리의 경우: 구간 업데이트(Range Update)
A[i], A[i+1], ... , A[j] 까지에 + k 를 해주어야 한다.
이를 B에 대해서 나타내면
B[i] => (A[i] + k) - A[i-1] = B[i] +k
B[i+1] => (A[i+1] + k) - (A[i] + k) = B[i+1]
.
.
.
B[j] => (A[j] + k) - (A[j-1] + k) = B[j]
B[j+1] => A[j+1] - (A[j] + k) = B[j+1] - k
즉, B[i]에는 + k, B[j+1]에는 -k만 해주면 구간 업데이트를 구간의 끝점에만 적용해주면 된다.
2번 쿼리의 경우 : 점 쿼리(Point query)
A[x]의 값은 B[1] + B[2] +...+ B[x]를 해주면 된다.
A[x] = A[1] + (A[2] - A[1]) + (A[3] - A[2]) + ... + (A[x-1] - A[x-2]) + (A[x] - A[x-1])
(파란 구간의 결국 서로 소거된다.)
즉, A를 B로 나타낸 펜윅 트리에서는 A원소의 값을 얻기 위해서 B의 1에서 x까지의 구간 합을 구해주면 된다.
그림으로 표현해보자.
일단 배열의 초기 값은 모두 0이다.

[3,5]의 구간에 x를 더한다고 하면
B[3] = A[3] - A[2] = x
B[6] = A[6] - A[5] = -x 이므로 각 해당 원소를 update해준다.
이 상황에서 A[4]의 값을 구하고 싶다면
B[4] + B[3] + B[2] + B[1]의 값을 구하면 된다.

B[4](= 0) + B[3](= 4) + B[2](= 0) + B[1](= 0) = 4
구간의 값 변경에는 원소의 값만 변경하고
오히려 원소 값을 구하기 위해 구간(부분) 합을 이용하는 것을 알 수 있다.
정리하면 펜윅트리로는 두 가지 구현, 점 업데이트(Point Update)와 구간 쿼리(Range query) 혹은
구간 업데이트(RangeUpdate)와 점 쿼리(Pointquery)이 가능 하지만
구간 업데이트와 구간 쿼리는 불가능하다.
하지만 세그먼트 트리를 변형해 두 가지 기능을 가능케 한 느리게 갱신되는 세그먼트 트리(Segment Tree Lazy Propagation)와 같이 펜윅트리에도 Lazy propagation의 적용이 가능하다. (물론 Lazy의 의미와는 다르게 구현되지만 일단 이렇게 부르자.)
Fenwick Tree Lazy propagation
펜윅 트리 Lazy propagation은 우리가 두 번째로 살펴본 구간 업데이트(RangeUpdate)와 점 쿼리(Pointquery)의 펜윅트리 두 개를 사용하여 구현한다.
Query 1 (구간 업데이트): A[L], A[L+1], ..., A[R]에 x를 더한다
Query 2 (구간 쿼리): A [L], A[L+1], ..., A[R]의 합을 출력한다.
(초기 값들은 0 이라 가정), 구간 [L,R]에 x를 더했을 경우
구간 [L,R] 사이의 k에 대해서 [1,k]의 구간 합은 (k-L+1)*x이다.
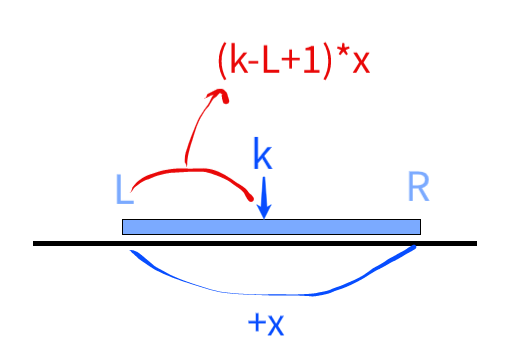
따라서 [L,R]의 사이에 존재하는 k에대해서 [1,k]까지의 합을
f(k) = k*x + (-L + 1)*x로 표현할 수 있다.
k에 대한 일차항인 k*x와 상수항인 (-L + 1)*x를 서로 다른 두 개의 펜윅 트리에 저장하자.
아래의 코드에서 일차항은 degree_tree, 상수항은 const_tree에 각각 저장한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class LazyFenwickTree{
public:
vector<int> degree_tree = vector<int>(TREESIZE); //일차항 저장
vector<int> const_tree = vector<int>(TREESIZE); //상수항 저장
void RangeUpdate(int L, int R, int x){
Update(degree_tree, L, x); //B[L] += x로 update
Update(degree_tree, R+1, -x); //B[R+1] -= x로 update
Update(const_tree, L, (-L + 1)*x);
Update(const_tree, L, (R)*x);
}
int RangeSum(int L, int R){
int ret = Sum(degree_tree,R)*R + Sum(const_tree,R); //[1,R]의 구간합
return ret -= Sum(degree_tree,L-1)*(L-1) + Sum(const_tree,L-1); //[1,L-1]의 구간합
}
int Sum(vector<int>& tree,int idx){
int ret = 0;
while(idx>0){
ret += tree[idx];
idx &= (idx -1);
}
return ret;
}
void Update(vector<int>& tree, int idx, int x){
while(idx <= tree.size()){
tree[idx] += x;
idx += (idx & -idx);
}
}
};
|
cs |
Sum()과 Update()함수는 기존의 펜윅 트리와 동일하지만
RangeUpdate(int L, int R, int x)은 구간의 업데이트
RangeSum(int L, int R)은 구간의 합을 구하기 위해 Sum()과 Update()를 사용하여 구현하였다.
일단 구간 업데이트 함수인 RangeUpdate를 살펴보자.
|
1
2
3
4
5
6
7
|
void RangeUpdate(int L, int R, int x){
Update(degree_tree, L, x); //B[L] += x로 update
Update(degree_tree, R+1, -x); //B[R+1] -= x로 update
Update(const_tree, L, (-L + 1)*x);
Update(const_tree, R+1, (R)*x);
}
|
cs |
Update(degree_tree, L, x); //B[L] += x로 update
=>A[L]이상의 위치 값들에 +x를 한다.
Update(degree_tree, R+1, -x); //B[R+1] -= x로 update
=> A[R+1]이상의 위치 값들에 -x를 한다.
위의 두 함수 호출은 일차항을 담당하는 degree_tree의 값을 변경한다.
구간의 양 끝의 원소(B[L], B[R+1])만 변경하여 [L,R]의 구간에 x값을 더하였다.

구간 쿼리(구간 합의 질의)가 없다면 이것만으로도 충분하지만 구간 쿼리를 위해 상수항을 담당하는 트리(const_tree)의 값을 변경해야 한다.
(*const_tree는 degree_tree와는 독립적임을 명심하고 생각해보자!*)
1. Update(const_tree, L, (-L + 1)*x);
f(k) = k*x + (-L + 1)*x 에서 알 수 있듯이 상수항은 구간 업데이트가 시작하는 L 위치에서부터 적용되어야 한다.
어떤 임의의 k를 선택하더라도 일차항은 변하지만 상수항은 (-L + 1)*x로 변하지 않는다.
따라서 상수항 트리의 L 이상의 구간부터는 (-L + 1)*x 을 더해주어야 한다.
2.Update(const_tree, R+1, (R)*x);
구간이 끝나는 R+1 이상부터는 상수항 (-L + 1)*x 은 적용되지 않는다.
이때 주의해야 하는 점이, 펜윅트리는 항상 부분 합(첫 원소에서부터 i개의 값)을 다룬다는 것이다!!
따라서 펜윅트리에서 Sum(부분합)의 질의가 R+1 이상의 위치로 주어진다면, 1에서부터 R+1이상의 값의 합을 반환하게 된다.
즉, R+1 이상에는 [L,R]의 구간 합(= (R-L+1)*x)이 포함된다.
1번 Update에서 우리는 이미 L이상의 위치들에 모두 (-L + 1)*x 을 더해주었다.
그렇다면 R+1 이상의 위치에서 +(R*x) 해준다면 R +1 이상의 값들은 (R-L+1)*x)로 업데이트된다.

이번에는 구간의 합을 구하는 RangeSum() 함수를 살펴보자.
|
1
2
3
4
|
int RangeSum(int L, int R){
int ret = Sum(degree_tree,R)*R + Sum(const_tree,R); //[1,R]의 구간합
return ret -= Sum(degree_tree,L-1)*(L-1) + Sum(const_tree,L-1); //[1,L-1]의 구간합
}
|
cs |
1. [1,R]의 구간합: Sum(degree_tree,R)*R + Sum(const_tree,R)
k까지의 부분합은 f(k) = x*k + (-L + 1)*x로 나타낼 수 있었다.
R까지의 부분합은 Sum(degree_tree,R)*R + Sum(const_tree,R) 에서
k에대한 일차항을 담당하는 Sum(degree_tree,R) * R 가 f(k)에서의 x* k 를 의미하고
상수항을 담당하는 Sum(const_tree,R)가 f(k)에서의 (-L + 1)*x를 의미한다.
Sum(degree_tree,R)*R + Sum(const_tree,R)
= (degree_tree에서의 A[R])*R + (const_tree에서의 A[R])
만약 RangeUpdate(L, R, x)가 이전에 한번 호출되었다면
degree_tree에서의 A[R] = x, const_tree에서의 A[R] = (-L +1)*x 이므로
Sum(degree_tree,R)*R + Sum(const_tree,R) = R*x + (-L +1)*x
2. [1,L-1]의 구간합: Sum(degree_tree,L-1)*(L-1) + Sum(const_tree,L-1)
동일하게 RangeUpdate(L, R, x)가 이전에 한번 호출된 상태라면
Sum(degree_tree,L-1)*(L-1) + Sum(const_tree,L-1)
= (degree_tree에서의 A[L-1])*(L-1) + (const_tree에서의 A[L-1])
= 0*(L-1) + 0 이다.
최종적으로 [1,R]의 구간합에 [1,L-1]의 구간합을 빼준 값이 [L,R]의 구간합이 된다.
R*x + (-L +1)*x - 0*(L-1) + 0 = R*x + (-L +1)*x
너무 이해가 안돼서 정리해보았는데, 여전히 어렵다..
제가 잘못 이해한 부분이 있을 수도 있으니 지적해주시면 감사하겠습니다.
참고한 게시글
Rebro님의 [알고리즘] Lazy Propagation (Segment / Fenwick Tree)
plzrun님의 구간 업데이트와 구간 합이 모두 O(logN)에 가능한 펜윅트리 (Fenwick Tree Lazy Propagation)
'알고리즘 공부 > 알고리즘 기법' 카테고리의 다른 글
| [절단선과 절단점] Articulation point, Bridge (Cut vertex, cut edge) (0) | 2021.03.14 |
|---|---|
| [임계 경로 알고리즘] Critical Path Method (백준-1948 해설) (0) | 2021.03.09 |
| [Union-Find] 유니온-파인드, 분리 집합 (백준 1717 - 집합의 표현 해설) (1) | 2021.02.28 |
| [자료구조] 트립(Treap) 구현 (376) | 2021.02.16 |
| [정수론] 에라토스테네스의 체와 소인수 분해 (0) | 2021.01.12 |