
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://www.acmicpc.net/problem/2613
2613번: 숫자구슬
첫째 줄에 구슬의 개수 N과 그룹의 수 M이 주어진다. 둘째 줄에는 각 구슬이 적혀진 숫자가 왼쪽부터 차례로 주어진다. N은 300 이하의 자연수, M은 N이하의 자연수이며, 구슬에 적혀진 숫자는 100
www.acmicpc.net
풀이
solved.ac 난이도: Gold 2
그리디 문제로 분류되었지만 이분 탐색을 응용한, parametric search를 사용해야 했던 문제이다.
이분 탐색(binary search)과 parametric search의 차이점은 라몽님의 게시글을 참조하자.
이진탐색(Binary Search)와 Parametric Search - 라몽의 배움일기
해당 문제의 풀이는 다음과 같다.
그룹들의 합 중에서 최댓값을 mid_num이라고 하자.
mid_num은 (left+right)/2로 구해진다.
일단 첫 번째 left(가능한 가장 작은 값)와 right(가능한 가장 큰 값)에는 적용 가능한 한계값을 넣어주자.
left(가능한 가장 작은 값)는 그룹들의 합 중에서 가장 작은 값이다.
이는 그룹을 이루는 구슬들이 단 한 개뿐일 때 가능하다. 즉, 구슬들 중에서 가장 큰 값이 left(최솟값)이 된다.
right(가능한 가장 큰 값)는 모든 구슬이 같은 그룹으로 속할 때이다. 즉, 모든 구슬 값의 합이다.
mid_num(그룹의 합 중 최댓값)은 (left+right)/2이다.
만약 구슬들을 차례로, 합이 mid_num이하가 되도록 그룹을 짓는다고 해보자.
1. 형성된 k개의 그룹이 M개 보다 많을 때

mid_num을 현재보다 높여야 그룹을 구성하는 구슬의 합(개수가)이 늘어나면서 총 그룹의 개수는 줄어들 수 있다.
2. 형성된 k개의 그룹이 M개 보다 많을 때
위와는 반대의 이유로 mid_num을 현재보다 줄여야 그룹의 개수가 늘어난다.
3. 형성된 k개의 그룹이 M개와 같을 때
형성된 그룹이 같은 개수일 때 mid_num이 정답이라고 생각할 수 있지만 mid_num을 조금 더 낮춰도 여전히 같은 개수의 그룹이 형성될 수 도 있다.(ex. mid_num은 10이지만 모든 구슬이 7의 값을 갖는다고 가정하면 mid_num은 7까지 줄어야 정답이 된다. )
따라서 k==M인 경우도 mid_num의 값을 줄여 보아야 한다.
이러한 3가지 경우에서 mid_num을 줄이거나 늘리는 작업은 이분 탐색과 같이 범위를 절반씩 줄여가며, 시간 복잡도 O(logN)을 형성해야 한다.
group_result를 형성된 그룹의 개수(k개)라고 하고 형성해야 하는 그룹의 개수를 group_num이라 하면 left혹은 right를 아래와 같이 설정해준다.
group_result> group_num인 경우(1번 case)
left = mid_num +1;
group_result <= group_num인 경우(2,3번 case)
right = mid_num -1;
만약 group_result <= group_num라면 right = mid_num -1이 되면서 범위가 반 줄어든다
그 후 mid2값에는 group_result> group_num라면 left=left = mid_num +1이 되면서 또다시 범위가 절반씩 줄어들게 된다.
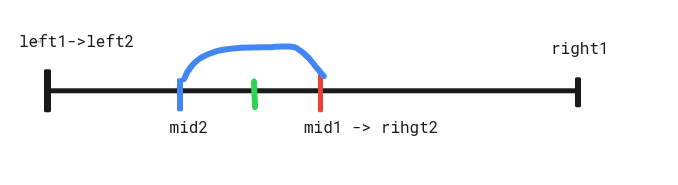
이러한 계산을 가장 가까운 값을 가질 때까지, 반복해주면 된다.
추가적으로 조심해야 하는 것이 있다.
3번 case에서 right = mid_num -1로 인해 mid값이 줄었는데 사실 정답은 mid_num이었다면 형성되는 그룹의 개수는 M보다 계속 많을 것이다(group_result> group_num). 따라서 아래의 코드처럼
|
1
2
3
4
5
6
7
|
if(group_result> group_num){
left = mid_num +1;
}else{
right = mid_num -1;
if(mid_num < answer)
answer = mid_num;
}
|
cs |
정답을 구한 후 각 그룹의 구슬 개수를 출력해 줄 때에도 조심해야 하는 것이 있다.
만약 구성해야 할 그룹의 개수가 남은 구슬 개수와 같다면 나머지 그룹은 모두 1개씩의 구슬만으로 구성되어야 한다.
이 경우는 아래의 MakeGroup(int limit) 함수를 참고하자.
코드
'알고리즘 공부 > 백준' 카테고리의 다른 글
| [백준] No.14889 - 스타트와 링크 (C++, 비트마스크) (0) | 2021.01.15 |
|---|---|
| [백준] No.2805 - 나무 자르기 (C++) (0) | 2021.01.10 |
| [백준] No.10165 - 버스 노선 (C++) (0) | 2021.01.07 |
| [백준] No.2513 - 통학버스 (C++) (0) | 2021.01.04 |
| [백준] No.11501 - 주식 (C++) (0) | 2021.01.03 |