
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://leetcode.com/problems/non-overlapping-intervals/
Non-overlapping Intervals - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
풀이
난이도: Medium
겹치지 않는 구간들만을 남기고 만약 겹치는 구간이 있다면 최소로 제거돼야 하는 구간의 수를 구하는 문제였다.
예를 들어 [1,2] [3,4] [1,4]의 구간이 있다면 [1,4]가 나머지 두 구간을 포함하며 겹친 상태가 된다.
겹치지 않도록 [1,2] [3,4]를 제거한다면 2개의 구간을 제거해야 하지만, [1,4]를 제거하면 1개만 제거할 수 있으므로 최소로 만들 수 있다.
처음에는 문제를 잘못 이해해여, [1,3] [2,4]와 같이 겹치더라도 합해져 더 큰 구간을 만드므로 둘은 overlapping되지 않는 거라고 생각했다.
하지만 단 하나의 구간이라도 겹치면 두 구간이 non-overlapping되는 것이므로 두 구간 중에 한 구간만 남겨 주어야 한다.
문제를 이해했다면 구현은 간단하다.
구현의 핵심은 반대로 겹치지 않는 구간을 세고, 전체 구간의 수에서 빼주는 것이다.
겹치지 않는 구간을 구하기 위해서는 먼저 구간의 end를 기준으로 오름차순으로 정렬한다.
이전 구간 end <= 다음 구간 start이라면 다음 구간과 겹치지 않는 것이다.
그렇다면 왜 end를 기준으로 오름차순 정렬을 해야 할까?
구간 [1,3] [2,4] [3,6] [4,5] [5,6]을 start를 기준으로 오름차순 정렬했다고 생각해보자.
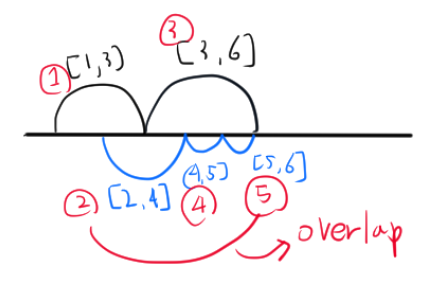
구간의 겹침을 판단할 때 [1,3]과 [2,4]가 겹치므로 [2,4]는 제거된다.
다음으로 [3,6은] 겹치지 않으므로 이 구간이 선택되면 [4,5] [5,6] 구간은 제거되어 최소로 구간을 제거하지 못한다.
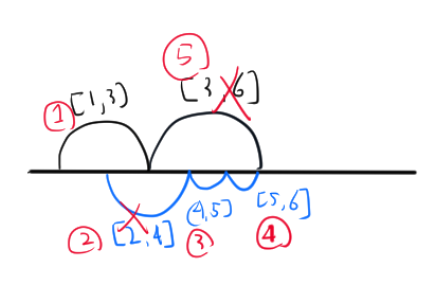
end를 기준으로 정렬한다면 [4,5] [5,6] 구간보다 [3,6] 구간이 뒤에 정렬되므로 겹치는 구간을 최소로 제거할 수 있다.
([3,6]이 [5,6]보다 앞으로 정렬되더라도 결과는 같음.)
코드
'알고리즘 공부 > LeetCode' 카테고리의 다른 글
| [LeetCode] 23. Merge k Sorted Lists (Java, C++) (0) | 2021.12.06 |
|---|---|
| [LeetCode] 21. Merge Two Sorted Lists (Java) (0) | 2021.12.05 |
| [LeetCode] 56. Merge Intervals (Java) (0) | 2021.11.19 |
| [LeetCode] 57. Insert Interval (Java) (0) | 2021.11.18 |
| [LeetCode] 128. Longest Consecutive Sequence (Java) (0) | 2021.11.16 |