
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://leetcode.com/problems/maximum-product-subarray/
Maximum Product Subarray - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
풀이
난이도: Medium
DP나 분할 정복으로 해결하려 했지만, 답을 알고 보니 사실 스위핑으로도 해결이 가능했다...
일단, 연속되는 부분 배열의 원소에 0이 포함된다면 다른 원소들의 값과는 상관없이 0이 된다.
따라서 최대 곱이 0이 아닌 이상, 0을 포함하지 않는 부분 배열이 답일 것이다. (음수가 최대 곱인 경우는 일단 제외)
그렇다면 다음과 같은 배열에서는 최대 곱이 나올 수 있는 부분 배열은 파란 부분일 것이다.

이러한 이유때문에 분할 정복 같은 것을 생각해보았지만,
왼쪽과 오른쪽에서 한번씩 스위핑 해주는 것으로 최대 곱을 구할 수 있다.
일단 0이 없는 배열을 생각해보자.
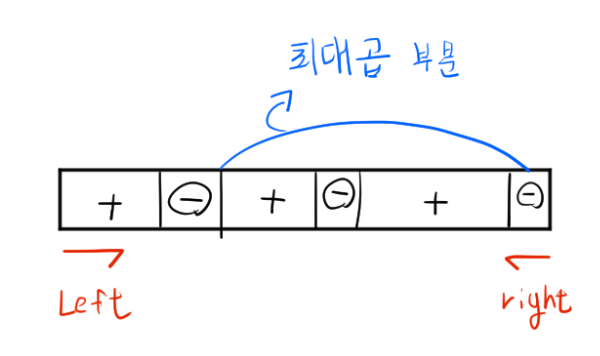
이때 양수는 1~10사이의 수이기 때문에 곱할 시에 항상 이득이 되므로 우리는 음수만 생각해주면 된다.
음수도 몇개가 있더라도 부분 배열 안에 짝수개만큼 포함이 되면 이득이 되므로 최대곱의 부분 배열에 음수가 있다면 짝수개만큼만 포함할 것이다.
결과적으로 최대 곱의 부분 배열은 위와같이 음수를 포함하기 직전인 범위일 것이다.
따라서 왼쪽이나 오른쪽에서부터 시작하는 부분 배열이 최대 곱의 부분 배열이 될 수밖에 없다.
부분 배열에 중간에 있는 경우는 있을 수 없는데,
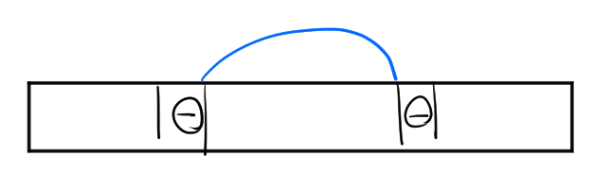
양수는 곱할 경우 항상 이득이기 때문에 중간에 최대 곱 부분 배열이 있다면 양 끝이 음수라는 의미이다.
하지만 음수 두개(짝수)를 배열에 포함시키면 결국 최대 곱에 항상 이득이되기 때문에 이런 경우는 있을 수 없다.
이제 배열에 0이 있는 경우를 생각해보자.
0은 부분 배열에 포함되면 곱이 0이 되므로 왼쪽과 오른쪽에서 곱을 진행하면서 0이 나온다면
0의 다음 부분 부터 새로운 부분 배열의 곱을 구하도록 만들어 주면 된다.
코드
'알고리즘 공부 > LeetCode' 카테고리의 다른 글
| [LeetCode] 33. Search in Rotated Sorted Array (C++) (0) | 2021.10.12 |
|---|---|
| [LeetCode] 153. Find Minimum in Rotated Sorted Array (C++) (0) | 2021.10.11 |
| [LeetCode] 53. Maximum Subarray (C++) (0) | 2021.10.09 |
| [LeetCode] 238. Product of Array Except Self (C++) (0) | 2021.10.03 |
| [LeetCode] 121. Best Time to But and Sell Stock (C++) (0) | 2021.10.03 |