
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://www.acmicpc.net/problem/17136
17136번: 색종이 붙이기
<그림 1>과 같이 정사각형 모양을 한 다섯 종류의 색종이가 있다. 색종이의 크기는 1×1, 2×2, 3×3, 4×4, 5×5로 총 다섯 종류가 있으며, 각 종류의 색종이는 5개씩 가지고 있다. <그림 1> 색종이를 크
www.acmicpc.net
풀이
처음 문제를 접하면 가장 큰 종이(5x5)부터 순서대로 대입해보면 되는 그리디 알고리즘처럼 느껴진다.
하지만 이러한 방식으로 문제를 해결하면 아래와 같은 예외적인 입력에서는 오답을 출력한다.
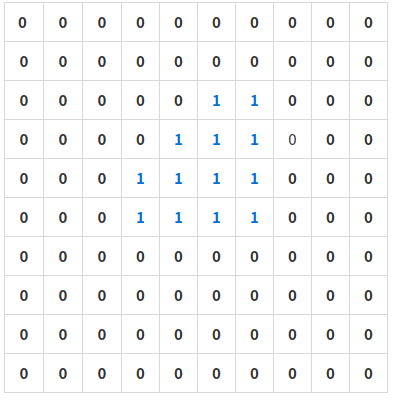
위와 같은 종이 판에 5-> 4-> 3-> 2-> 1 의 순서로 종이를 대입하게 되면
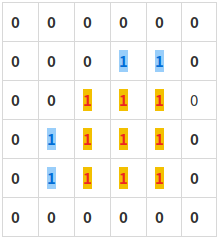
위와 같이 3x3 크기의 종이 1개가 먼저 배치된 후 나머지는 1x1 크기의 종이 4개가 채우게 된다.
즉, 사용한 색종이의 개수는 5개이다.
하지만 해당 결과의 최솟값은 아래와 같이 2x2 크기의 종이 3개와 1x1 종이 1개, 총 4개를 사용한 것이다.
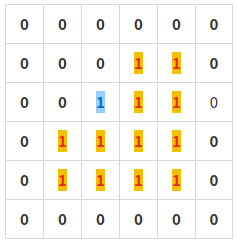
따라서 큰 순서대로 집어넣어 보는 그리디 알고리즘은 틀렸다.
그렇다고 이번에는 작은 순서대로 넣어보아도 위와같이 최선 값을 구할 수 없다.
우리는 여러가지 입력에서도 최솟값을 구해야 하기 때문에 모든 종이판을 순회하며 모든 크기의 종이를 넣어보아야 한다.
모든 배열을 순회하면서 만약 해당 [row][col]이 1이라면 특정 크기의 종이를 넣어보고 다음 1의 칸으로 재귀 호출을 진행한다.
즉 브루트 포스와 DFS알고리즘을 결합시킨 문제이다.
해당 문제의 구현의 핵심은 두 가지이다.
첫째, board[row][col] 를 특정 크기의 종이로 채울 수 있다면 종이의 크기만큼 채워주고, 재귀 호출로 다음 값을 찾은 후에는 다시 board의 값을 복구 시켜야 한다. 이는 아래의 두 가지 함수로 구현하였다.
해당 위치부터 paperSize 크기의 종이를 채울 수 있는지 확인하는
CheckPosFill(int paperSize, int r, int c);
매개 변수 fill의 값에 따라 paperSize크기만큼 board를 1로 채우거나 0으로 채우는
void FillBlocks(int paperSize, int r, int c,int& remainedBlocksNum, bool fill);
둘째, 브루트 포스의 특성상 너무 긴 실행시간이 걸릴 것을 대비하여, 최솟값minUsedPaperNum 보다 더 많은 색종이를 사용했다면 재귀 호출을 끝내는 기저 사례를 마련하는 것이다.
이는 사용된 종이의 개수 usedPaperNum와 minUsedPaperNum를 비교하여 usedPaperNum가 더 크다면 재귀를 바로 종료하여 구현한다.
코드
해당 코드를 구현하다가 다음 row,col로 넘어가는 것을 아래와 같이 for문으로 구현했었다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
for(int r=startRow; r<boardSize ; ++r){
for(int c=0; c< boardSize ; ++c)
if(board[r][c]==1){
for(int paperSize=5; paperSize>0 ; --paperSize)
if(remainedColoredPaper[paperSize] >0 && remainedBlocksNum >= paperSize*paperSize)
if(r+paperSize<=boardSize && c+paperSize<=boardSize){
if(CheckPosFill(paperSize, r, c)){
--remainedColoredPaper[paperSize];
FillBlocks(paperSize,r,c,remainedBlocksNum,true);
FillColoredPaperDfs(r,remainedBlocksNum,usedPaperNum +1);
FillBlocks(paperSize,r,c,remainedBlocksNum,false);
++remainedColoredPaper[paperSize];
}
}
}
|
cs |
하지만 예제 입력에서 지속적인 시간 초과가 나와서 계속 고민하다 결국 정답 코드와 같이 구현을 했다.
나중에 다시 곰곰이 보다가 for문에서 board[r][c]==1 에 해당하는 지점을 발견하여 5가지 종이를 넣어보고 마지막으로 2중 for문을 모두 탈출하는 코드를 구현하여야 했는데 그지점을 빠트려서 무한반복에 빠진 것이었다. 특히 요즘 브루트 포스 문제를 풀면서 이와 같은 실수가 많이 발생하는 것 같다. 주의하자.
'알고리즘 공부 > 백준' 카테고리의 다른 글
| [백준] No.10830 - 행렬 제곱 (C++) (0) | 2020.11.07 |
|---|---|
| [백준] No.1780 - 종이의 개수 (C++) (0) | 2020.10.30 |
| [백준] No.1543 - 문서 검색 (C++) (0) | 2020.10.26 |
| [백준] No.17135 - 캐슬 디펜스 (C++) (0) | 2020.10.25 |
| [백준] No. 1038 - 감소하는 수 (C++) (0) | 2020.10.24 |