
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://www.acmicpc.net/problem/6086
6086번: 최대 유량
첫째 줄에 정수 N (1 ≤ N ≤ 700)이 주어진다. 둘째 줄부터 N+1번째 줄까지 파이프의 정보가 주어진다. 첫 번째, 두 번째 위치에 파이프의 이름(알파벳 대문자 또는 소문자)이 주어지고, 세 번째 위
www.acmicpc.net
풀이
solved.ac 난이도: Platium 4
이름부터가 최대 유량인 최대 유량 문제.
최대 유량 알고리즘과 이번 풀이의 기본 지식을 알기 위해 다음 게시글을 참고 하자.
[네트워크 유량] Network Flow(최대 유량, 최소 컷) 알고리즘
기본적인 최대 유량 알고리즘을 적용하기에는 약간 다른 점이 있는데
파이프는 양방향으로 존재하고 같은 두 정점이 여러 간선으로 이어질 수 있다는 점이다.
두 정점 사이에 여러 간선이 이어져있는 것은 생각보다 간단히 해결할 수 있는데,
문제의 설명처럼 여러 개의 파이프가 병렬로 연결되어 있다면 단순히 각 용량을 합한 하나의 파이프로 만들어 주면 된다.

이제 양방향 간선에 대해 생각해보자.
최대 유량에 대해서 설명했던 예제들은 모두 단방향 간선이었는데,
최대 유량 알고리즘의 구현을 위해 역방향으로 용량이 0인 유령 간선을 생성해 주었다.
하지만 이번에는 역방향에도 동일한 용량을 가지는 간선을 생성시켜 주어야 한다.
이러한 경우에도 최대 유량 알고리즘인 포드-풀커슨 알고리즘이 정상적으로 진행되는지 확인해보자.
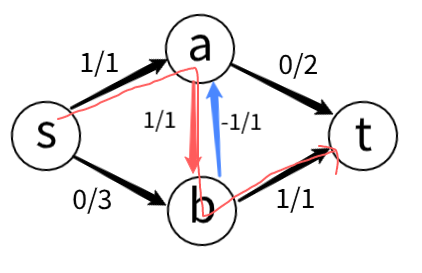
위와 같은 그래프에서 s->a->b->t 방향으로 1만큼의 유량이 흐른다면 역방향인 b->a 간선에는
-1만큼의 유량이 흐를 것이다.
이때 b->a 간선의 잔여 용량은 다음과 같다.
r(b, a) = c(b, a) - f(b, a) = 1 -(-1) = 2
따라서 용량은 1인 간선에 최대 2만큼의 유량을 보낼 수 있다!
말이 안 되는 듯 하지만 유량의 대칭성에 의해 a->b의 유량이 상쇄되기 때문에 가능하다.
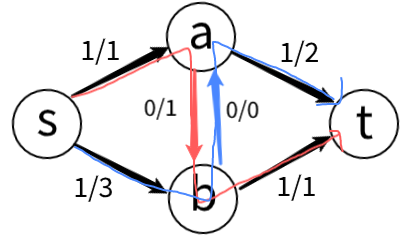
증가 경로인 s->b->a->t로 2만큼의 유량을 흘려준다면 유량의 상태는 다음과 같이 변한다.

a->b의 flow는 2만큼 감소하여 -1이 된다.
생각해보면 파이프를 양방향 간선으로 표현한 것뿐이지 하나의 파이프에서 서로 다른 두 가지 방향으로 유량이 흐를 수는 없다.
알고리즘을 진행하다 보면 결국 한쪽 방향의 유량이 양수가 되는 것이 최대 유량을 구하는 방법이 될 수밖에 없다.
위와 같은 유량의 상태는 아래와 같이 증가 경로를 찾는 것과 동일한 상태이다.

이러한 양방향 간선은 단방향 간선과 다르게, 역 방향 간선도 용량(0보다 큰)을 가지므로 더 큰 유량을 흘려줄 수 있는 가능성을 가지고 있다.
단방향 간선으로 구현된 경우 최대 유량은 2에 불과 하지만 양방향의 경우 최대 유량은 3이다.
코드
'알고리즘 공부 > 백준' 카테고리의 다른 글
| [백준] No.2316 - 도시 왕복하기 2 (C++, 최대 유량, 정점 분할) (0) | 2021.06.02 |
|---|---|
| [백준] No.1420 - 학교 가지마! (C++, 최소 컷, 최대 유량, 정점 분할) (0) | 2021.06.02 |
| [백준] No.4792 - 레드 블루 스패닝 트리 (C++, MST) (0) | 2021.05.27 |
| [백준] No.1185 - 유럽여행 (C++, MST 크루스칼) (0) | 2021.05.24 |
| [백준] No.2887 - 행성 터널 (C++, 크루스칼 MST) (0) | 2021.05.23 |