
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://algospot.com/judge/problem/read/HANOI4
algospot.com :: HANOI4
하노이의 네 탑 문제 정보 문제 하노이의 탑은 세 개의 기둥에 꽂혀 있는 N개의 원반을 가지고 하는 게임입니다. N개의 원반은 크기가 모두 다르며, 게임의 시작 때는 그림과 같이 맨 왼쪽의 기둥
algospot.com
풀이
종만북 난이도: 중
재귀 함수 문제의 대표 격인 하노이 탑 문제에 기둥을 1개 더 추가하여 4개인 상태로 해결하는 문제이다.
이번 문제의 핵심은 각 기둥에 꽂혀있는 원판들의 상태를 어떻게 저장하느냐이다.
단순히 4개의 기둥들이 어떤 원판을 가지는지 stack을 사용하여 표현한다면
4개의 스택(각각의 기둥)을 가지는 구조체로 나타낼 수 있을 것이다.
|
1
2
3
|
struct State{
stack<int> st[4];
};
|
cs |
구현은 하나의 상태를 표현하는데 메모리를 많이 소비할 뿐만 아니라
각 상태를 정점으로 나타낸 너비 우선 탐색에서는 해당 상태의 최단 거리를 저장하기 위해 map 자료구조를 사용한다.
map 자료구조는 배열보다 훨씬 비효율적이기 때문에 메모리 초과 뿐만아니라 시간 초과를 유발한다.
따라서 이러한 상태 표현의 압축에 특화된 비트마스크 기법을 적용하자.
비트 마스크로 기둥들의 상태를 표현하는 방법은 두 가지가 있다.
1. 각 기둥이 가지는 원판을 비트로 나타낸다.
예를 들어 원판이 4개인 경우 각 기둥마다 순서대로 1, 2, 3, 4 사이즈의 원판을 가지면 다음과 같이 표현된다.
1000 0100 0010 0001
이런 식으로 표현하면 원판의 최대 개수인 12개인 경우 12*4 = 48개의 비트로 모든 기둥의 상태가 표현 가능하다.
2. 각 원판이 꽂혀있는 기둥을 비트로 나타낸다.
기둥의 개수는 4개이므로 각 기둥을 0(00), 1(01), 2(10), 3(11)로 표현할 경우 위와 같이 원판이 꽂혀있는 상태는
11 10 01 00
으로 표현된다.
이런 표현법은 최대 12*2 = 24개의 비트로 모든 상태를 표현 가능하여 1번의 방법보다 2배 더 적은 메모리를 사용한다.
특히 24개의 비트는 int형의 범위 내에서 표현 가능 하지만 48개의 비트는 long long형으로 표현해야 하므로 낭비하는 메모리가 크다.
이제 각 상태를 int형만으로도 표현할 수 있으므로 최단 거리를 int형 배열로 저장해낼 수 있다.
자, 이제 각 기둥의 맨 위의 원판을 다른 기둥으로 이동시키며 BFS를 진행하면 될까?
안타깝지만 지금 까지의 최적화에도 여전히 시간 초과가 발생한다.
따라서 양방향 탐색(Bidirectional serach)이라는 추가적인 최적화를 진행하자.
양방향 탐색(Bidirectional serach)
양방향 탐색은 목표 상태가 지정되어있는 경우 시작점과 목표점에서 동시에 BFS을 진행한다.
단, 목표 상태에서도 역방향으로 올라갈 수 있는 양방향 그래프에서 적용 가능하다.
이번 문제는 목표 상태인 오른쪽의 기둥에 모든 원판이 쌓여있더라도 역방향으로 원판을 다른 기둥으로 이동시킬 수 있으므로 양방향 탐색이 가능하다.
양방향 탐색의 효율성을 간단히 그림으로 표현해보면 다음과 같다.
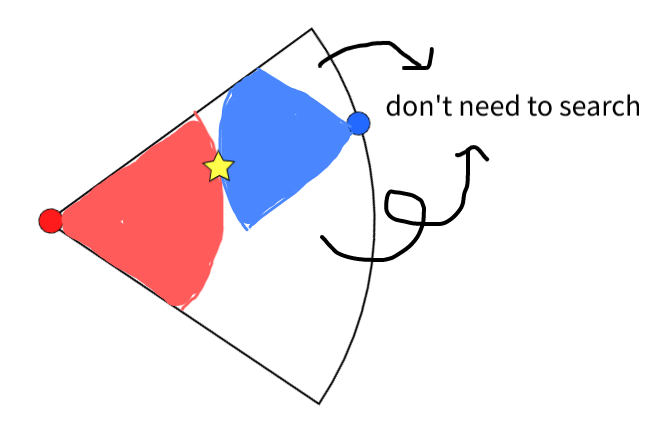
BFS는 탐색 분기 수를 n이라 할 때 깊이가 하나 깊어질수록 탐색해야하는 정점은 n배만큼 늘어난다.
따라서 깊이(d)가 깊어질 수록 탐색할 정점들은 d^n개로 지수 증가한다.
이러한 상황은 탐색 시간은 물론 BFS를 진행하기 위해 저장하는 정점들의 양도 지수 증가하여 메모리의 사용양도 많아진다.
하지만 목표 정점에서도 반대로 BFS를 진행한다면 목표까지의 깊이(최단 거리 d)는 반으로 줄일 수 있다.
이러한 최적화는 깊이(d)가 깊어질수록 효과가 극대화된다.
따라서 이번 문제의 시간 초과를 극복하기 위해 정해진 목표 상태(오른쪽 맨 끝 기둥에 모든 원판이 존재하는 상태)를 초기 queue에 넣어주어 BFS를 진행하자.
단, 역방향으로 진행해 방문한 정점과 정방향으로 진행하여 방문한 정점의 구별을 위해(만나는 지점을 확인해야 하므로)
정방향 정점 방문까지의 최단 거리는 양수, 역방향 정점 방문의 최단 거리는 음수로 표현하자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
inline int Sign(const int& x){
if(!x)
return 0;
return x > 0 ? 1 : -1;
}
inline int IncrAbsolute(const int& x){
if(x < 0)
return x - 1;
return x +1;
}
inline int GetColumnIdx(int state, const int& size){
return (state>>(size*2)) & 3;
}
inline int SetState(int state, int size, const int& column_idx){
return ( ( state & ~(3<<(size*2)) ) | (column_idx<<(size*2)) );
}
int SolveHanoi4(const int& start_state , const int& dest_state){
queue<int> que;
memset(visited, 0 , sizeof(visited));
if(start_state == dest_state)
return 0;
que.push(start_state);
que.push(dest_state);
visited[start_state] = 1;
visited[dest_state] = -1;
int now_state;
int visited_order;
while(1){
now_state = que.front();
que.pop();
visited_order = visited[now_state];
int columns_top[4] ={discus_num, discus_num, discus_num, discus_num};
for(int disc_size =0 ; disc_size<discus_num ;++disc_size ){
int col_idx = GetColumnIdx(now_state, disc_size);
columns_top[col_idx] = min(columns_top[col_idx], disc_size);
} //기둥들의 가장 위의 원반의 크기를 구하기
for(int col_idx =0; col_idx<4 ; ++col_idx){
if(columns_top[col_idx] == discus_num)
continue;
for(int dest_col =0; dest_col<4 ; ++dest_col)
if(columns_top[col_idx] < columns_top[dest_col]){
int next_state = SetState(now_state,columns_top[col_idx] , dest_col );
if(visited[next_state] == 0){ //방문하지 않은 경우
que.push(next_state);
visited[next_state] = IncrAbsolute(visited_order);
}else if(Sign(visited[now_state]) != Sign(visited[next_state])){
return abs(visited_order) + abs(visited[next_state]) -1;
}
}
}
}
return -1;
}
|
cs |
참조 서적: 알고리즘 문제 해결 전략(구종만 저)
코드
'알고리즘 공부 > 알고스팟' 카테고리의 다른 글
| [알고스팟] NTHLON - 철인 N종 경기 (C++, 다익스트라) (0) | 2021.05.07 |
|---|---|
| [알고스팟] FIRETRUCKS - 소방차 (C++, 다익스트라) (0) | 2021.05.02 |
| [알고스팟] CHILDRENDAY - 어린이날 (C++, BFS) (0) | 2021.04.24 |
| [알고스팟] SORTGAME - Sorting Game (C++, BFS) (0) | 2021.04.20 |
| [알고스팟] GALLERY - 감시 카메라 설치 (C++, 트리의 최소 지배 집합) (0) | 2021.04.10 |