
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://www.acmicpc.net/problem/10265
10265번: MT
남규는 동기들과 엠티를 가기 위해 버스를 대절했다. 그런데 과사의 실수로 대절버스의 인원이 잘못되어 남규의 동기들을 모두 태울 수 없었다. 이 와중에 동기들은 화를 내며 다음과 같은
www.acmicpc.net
풀이
solved.ac 난이도: Platium 4
SCC로 새롭게 구성한 컴포넌트 별로 최대, 최소 인원을 파악해 배낭 문제로 값을 구해야 했던 문제로 굉장히 어려웠다..
일단 인원 마다 같이 가고 싶은 인원(pick)을 가리키도록 그래프로 표현해보자.
1번 인원이 2번 인원과 가고 싶다면 다음과 같이 표현된다.
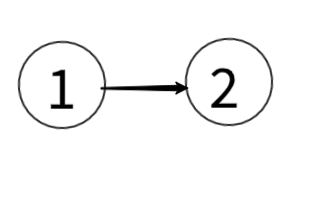
관계를 이런식으로 나타냈을 때 예제의 입력인
12 3
2 3 4 5 6 7 4 7 8 8 12 12
을 그래프로 표현하면 다음과 같다.
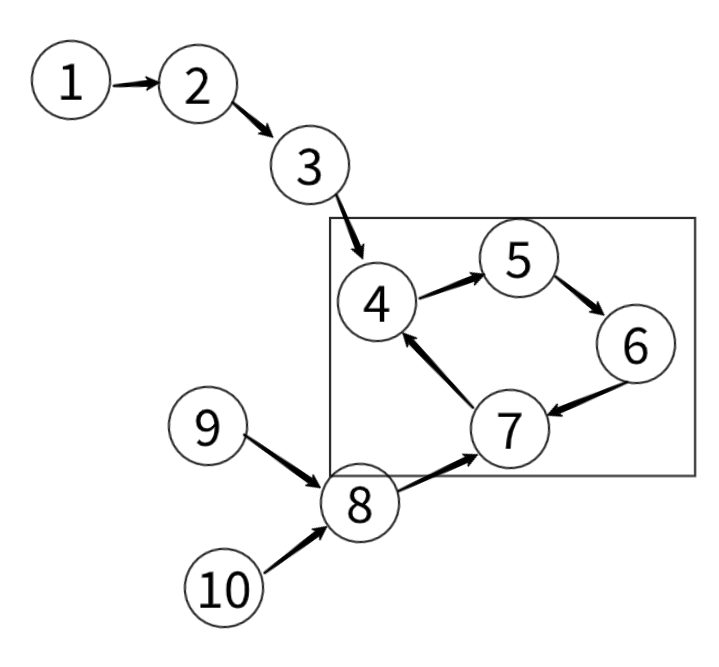
여러 관계들을 표현하면 알 수 있는 사실은
바로 각 컴포넌트들의 최하위 노드들끼리는 서로 같이 가고싶은 인원들의 관계가 사이클을 이룬다는 것이다.
그리고 사이클이외의 상위 노드들은 모두 사이클에 포함되지 않고 각자의 하위 노드(같이 가고 싶은 인원)만을 가리킨다.
그 이유는 만약 상위 노드들끼리도 사이클을 이룬다면 사이클에서 빠져나오는 진출 간선이 있어야 하지만
각 노드(인원)들은 서로 한 노드만을 가리킬 수 있으므로 진출 차선은 존재할 수 없다.
따라서 컴포넌트의 최하위 노드들끼리만 사이클을 이룰 수 있다.
상위 노드들은 각각 한 개의 노드를 가리키므로 만약 상위 노드(인원)를 버스에 태우고 싶다면 간선끼리 연결된 노드는 모두 포함되어야 한다.
이때 사이클에 포함된 노드들은 항상 모든 노드들과 연결되어 있으므로 누구를 데려가고 싶든 항상 하위의 사이클에 인원들은 모두 데려가야 한다.
예를 들어 9번 인원을 버스에 태우고 싶다면 원하는 사람들이 연결된 다음 인원들을 모두 데려가야 한다.

이런 식으로 각 인원을 한 명 한 명 선택하다 보면 결국
해당 컴포넌트에서 최소로 버스에 태울 수 있는 인원은 사이클을 이루는 노드들의 개수이고
상위의 노드들은 한 개씩 모두 선택해 태울 수 있으므로
위의 컴포넌트에서는 4, 5, 6, 7, 8, 9, 10 명의 인원들을 같이 가고 싶어 하는 관계를 유지하여 태울 수 있다.
즉, 컴포넌트마다 사이클을 이루는 인원을 최소 인원으로, 컴포넌트의 노드 개수를 최대 인원으로 하여 버스에 태울 수 있다.
이러한 구현에서 중요한 것은 사이클의 크기를 구하는 것인데
이때 사용하는 알고리즘이 강결합 컴포넌트(Strongly Connected Component, SCC) 알고리즘이다.
단, 이번 문제에서 컴포넌트마다 DFS 순회로 모든 노드를 돌 수 있으려면 진입 차수(indegree)가 0인 노드가 한 개 이어야 한다.
이를 위해 관계를 반대로 선택받은 인원이 선택한 인원을 가리키도록 그래프를 역전시키면 항상 SCC가 컴포넌트의 루트에 존재하여 모든 노드를 DFS로 방문할 수 있다.
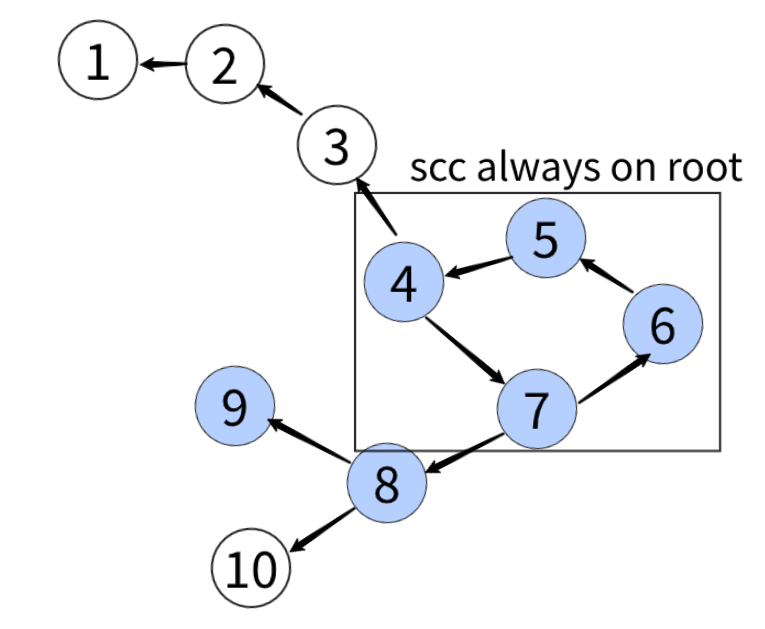
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
int MakeMaxMinOfComponent(int idx, bool is_root, int parent_scc){ //각 컴포넌트의 최대 최소 인원을 구하기
visited[idx] = true;
int ret =0;
if(is_root) //루트 노드의 SCC크기가 최소
ret = component_min_max[component_order].first = scc_size[scc_label[idx]];
if(parent_scc != scc_label[idx]) //부모 노드와 다른 SCC라면 사이클에 없는 노드
ret = scc_size[scc_label[idx]];
int next_idx;
for(int i=0 ; i<adj[idx].size() ; ++i){
next_idx = adj[idx][i];
if(visited[next_idx] == false)
ret += MakeMaxMinOfComponent(next_idx, false, scc_label[idx]);
}
if(is_root)
component_min_max[component_order].second = ret;
return ret;
}
int main(){
ios_base::sync_with_stdio(0);
cin>>people_num>>bus_capacity;
adj = vector<vector<int>>(people_num+1);
int pick;
for(int idx=1; idx<=people_num ; ++idx){
cin>>pick;
adj[pick].push_back(idx);
}
TarjanSCC();
component_min_max = vector<pair<int,int>>(scc_order);
visited = vector<int>(people_num+1, false);
for(int idx=1; idx<=people_num ; ++idx){
if(scc_indegree[scc_label[idx]]==0 && visited[idx] == false){
MakeMaxMinOfComponent(idx, true,scc_label[idx]);
++component_order;
}
}
memset(dp, -1 ,sizeof(dp) );
cout<<KnapsackDFS(0,bus_capacity)<<'\n';
return 0;
}
|
cs |
이제 각 컴포넌트 별로 최대, 최소 인원을 구했으니 이를 배낭 알고리즘(Knapsack)으로 버스에 태울 수 있는 최대 인원을 구하자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int KnapsackDFS(int component_idx, int remain_cap){
if(component_idx >=component_order)
return 0;
int& ret = dp[component_idx][remain_cap];
if(ret != -1)
return ret;
ret = KnapsackDFS(component_idx+1,remain_cap ); //해당 컴포넌트에서는 아무도 태우지 않음
for(int i=component_min_max[component_idx].first; i<=component_min_max[component_idx].second ; ++i){
if(i>remain_cap)
break;
ret = max(ret, KnapsackDFS(component_idx+1,remain_cap-i ) + i); //최소 인원에서 최대 인원까지 태워봄
}
return ret;
}
|
cs |
참조 게시글
코드
'알고리즘 공부 > 백준' 카테고리의 다른 글
| [백준] No.5214 - 환승 (C++, BFS, 더미 노드) (0) | 2021.04.21 |
|---|---|
| [백준] No.5014 - 스타트링크 (C++, BFS) (0) | 2021.04.20 |
| [백준] No.3109 - 빵집 (C++, DFS) (0) | 2021.04.15 |
| [백준] No.16915 - 호텔 관리 (C++, 2-SAT) (0) | 2021.04.14 |
| [백준] No.3648 - 아이돌 (C++, 2-SAT) (0) | 2021.04.14 |