
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
[2-SAT] 2 - Satisfiability Problem / 충족 가능성 문제 (알고스팟 회의실 배정 풀이)
EVEerNew 2021. 4. 11. 23:51
Boolean 변수들에 대해서 참, 거짓의 결정을 여러 번 해야 하는 문제를 충족 가능성 문제(Satisfiability Problem, SAT)라고 합니다.
특히 그중에 선 괄호 안의 각 절(clause)에 최대 두 가지 변수만이 존재하는 경우를 2-SAT 문제라고 합니다.
예를 들어 다음과 같은 식은 각 절에 두 가지 변수를 가지고 있습니다.
(A || B) && (B || C) && (C || D)
(이처럼 각 절들이 && 로 연결된 수식을 논리곱 정규형(Conjunctive normal)이라고 합니다.)
이제 2-SAT로 해결해야 하는 문제인 알고스팟 회의실 배정(MEETINGROOM) 문제를 풀면서 2-SAT에 대하여 알아봅시다.
문제
https://algospot.com/judge/problem/read/MEETINGROOM
algospot.com :: MEETINGROOM
회의실 배정 문제 정보 문제 회사가 빠르게 성장하면서 사람들이 늘어나면 가장 먼저 부족해지는 것이 화장실과 회의실입니다. 빠르게 확장하고 있는 치선이네 회사에서는 최근 회의실이 문제
algospot.com
풀이
종만북 난이도: 상
각 팀들은 주간 회의나 월간 회의 중에 하나를 회의실을 배정받아 진행해야 합니다.
특정 팀의 주간회의를 A, 월간 회의를 B라고 하면 둘 중 하나는 진행해야 하므로 다음과 같은 논리식으로 표현됩니다.
(A || B)
위의 논리식이 참이 되려면
- A가 진행되지 않으면 B가 진행되어야 합니다.
- B가 진행되지 않으면 A가 진행되어야 합니다.
이러한 표현을 'p이면 q이다'의 필요조건과 충족 조건 명제로 나타내면 다음과 같이 나타낼 수 있습니다.
- !A => B
- !B => A
이때의 각각의 변수(A,!A...)들을 정점으로 나타내고 화살표를 간선으로 나타내면 바로 그래프의 형태가 됩니다.
이처럼 논리식의 변수들의 요구 조건을 나타낸 그래프를 함축 그래프(implication graph)라고 합니다.
이번 문제에서 각 팀의 두가 종류의 회의는 반드시 하나는 진행해야 합니다.
따라서 각 팀의 주간, 월간 회의를 모두 (A || B) 로 표현해줍니다.
예를 들어 예제의 회의 시간
3
2 5(A0) 6 9(A1)
1 3(A2) 8 10(A3)
4 7(A4) 11 12(A5)
을 함축 그래프로 나타내면

다음으로는 서로 시간대가 겹치는 두 가지 회의는 동시에 진행될 수 없으므로
시간 대가 겹치는 회의 A와 B는 다음과 같이 논리식으로 표현됩니다.
(!A || !B)
즉,
A가 진행되면, B는 진행되서는 안 되고 A => !B
B가 진행되면, A는 진행되서는 안 됩니다. B => !A
단 B가 진행이 안된다고 A가 진행되어야 하지 않습니다.(가능한 최대한 회의를 개최하는 문제가 아님)
이러한 경우는 필요충분조건일 때만 성립됩니다.
물론 A와 B 두 회의 모두 진행되지 않아도 됩니다.
이를 함축 그래프에 추가하면 다음과 같습니다.

정점의 쌍인 A와 !A는 하나는 참, 하나는 거짓으로 분류되며
위에서 설명했듯이 'p이면 q이다'의 명제를 간선으로 표현했으므로
참 정점에서 거짓 정점으로 가는 경로는 없습니다. (p가 참이면 q도 참이어야만 하기 때문)
하지만 명제에 의해
참 -> 참
거짓 -> 참
거짓 -> 거짓
이 되는 경우는 가능합니다.
이렇게 나타낸 그래프를 강결합 컴포넌트(Strongly Connected Component) SCC 로 묶어 나타낸 면 아래와 같습니다.
(2-SAT문제를 해결하기 위해 SCC에 대한 이해는 필수적이니 먼저 공부하고 옵시다.)

답을 가지는 2-SAT 문제에서는 위의 처럼 SCC로 나타낸 그래프에서는 SCC에 속한 변수들의 반대 값들이 정확이 대칭되는 SCC가 존재합니다.
SCC로 나타낸 그래프는 DAG(사이클이 없는 그래프)로 표현됩니다.
또한 참 정점에서 거짓 정점으로 진행할 수 없기 때문에 같은 SCC의 정점들은 같은 값을 가져야만 합니다.
서로 다른 SCC가 간선으로 연결된 경우, 1번 SCC에서 2번 SCC로 가는 간선이 있을 때
2번 SCC는 1번 SCC방향인 역 방향으로 이동할 수 없기 때문에
1번 SCC의 정점들이 거짓의 값을 갖는다면 2번 SCC는 거짓 혹은 참이 될 수 있지만
1번 SCC가 참의 값을 갖는다면 1번 SCC는 참 값만을 가져야만 합니다.
이제 진입 차수(indegree)가 0인 상위 정점(SCC를 정점으로 생각)에서부터 해당 정점을 참으로 할지 거짓으로 할지 결정하면서 진행합시다.(해당 SCC가 결정되면 대칭되면 SCC는 자동으로 값을 가지게 됩니다.)
방금 설명했듯이 결정되지 않은 SCC를 만나면 일단 항상 거짓으로 분류해야 잃는 것이 없으니 항상 거짓으로 설정합시다.
본격적이 코드의 구현은 다음과 같습니다.
함의 그래프 만들기
팀마다 2개의 회의와 각 회의는 A와 !A인 두 가지 변수를 가지므로 총 4*(team_num)개의 정점이 존재합니다.
각 회의를 수열(일렬)로 표현한다고 합시다.
i번째 회의는 회의가 열리는 변수 A와 열리지 않는 변수 !A를 가집니다.
따라서 회의마다 두 가지 변수가 생기고 이를 수열에 일렬로 저장하면
A는 2*i, !A는 2*i + 1에 상태가 저장됩니다.
이런식으로 모든 변수의 인덱스 번호를 구할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
int team_num;
vector<pair<int,int>> meetings;
vector<vector<int>> adj;
vector<int> scc_label;
bool Disjoint(const pair<int,int>& a, const pair<int,int>& b ){
return a.second <= b.first || b.second <= a.first;
}
void MakeGraph(){
adj = vector<vector<int>>(meetings.size()*2);
int month_meeting=0;
for(int week_meeting=0; week_meeting<meetings.size() ; week_meeting+=2){
month_meeting = week_meeting +1;
adj[week_meeting*2+1].push_back(month_meeting*2); //!A => B
adj[month_meeting*2+1].push_back(week_meeting*2); //!B => A
adj[week_meeting*2].push_back(month_meeting*2+1); //A => !B
adj[month_meeting*2].push_back(week_meeting*2+1); //B => !A
}
for(int i=0; i<meetings.size() ; ++i)
for(int j=0; j<i ; ++j){
if(!Disjoint(meetings[i],meetings[j])){ //회의가 겹치는 경우
adj[i*2].push_back(j*2 +1);
adj[j*2].push_back(i*2+1);
}
}
}
|
cs |
일단 팀마다 두 종류의 회의 중 하나를 진행해야 합니다.
이때의 절은 위에서 확인하였듯이 아래와 같습니다.
(A(=week_meeting)) || B(=month_meeting))
따라서 해당 정점의 간선이 아래와 같이 향하도록 adj에 추가해줍니다.
!A => B adj[week_meeting*2+1].push_back(month_meeting*2);
!B => A adj[month_meeting*2+1].push_back(week_meeting*2);
그런데 사실 위의 함의 그래프에 표현했던 것과 달리
문제를 잘 읽어보면 두 종류의 회의를 모두 진행해서는 안되고 팀마다 오직 한가지 회의만을 진행하도록 설명하고 있습니다.
각 팀에 두 시간 중 하나를 배정해서 회의 시간이 서로 겹치지 않도록 할 수 있는지 계산하는 프로그램을 작성하세요.
따라서 해당 절을 추가해 주어 함의 그래프를 만들어 줍니다.
(!A || !B)
A가 진행되면, B는 진행되서는 안 되고 A => !B
adj[week_meeting*2].push_back(month_meeting*2+1);
B가 진행되면, A는 진행되서는 안 됩니다. B => !A
adj[month_meeting*2].push_back(week_meeting*2+1);
다음으로는 겹치는 회의를 표현한 절들을 통해 간선을 이어줍시다.
이는 (!A || !B) 절의 표현법과 동일합니다.
2-SAT 문제 답 구하기
이제 함의 그래프를 만들었으니 2-SAT 문제의 답을 구해봅시다.
일단 설명했듯이 그래프를 같은 SCC끼리 묶고 각 정점이 어떤 SCC에 속하는 scc_label에 저장합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
vector<int> visited_order;
stack<int> st;
int order=0, scc_order=0;
int FindSCC(int now_node){
int min_order = visited_order[now_node] = ++order;
int next_node;
st.push(now_node);
for(int i=0; i<adj[now_node].size() ; ++i){
next_node = adj[now_node][i];
if(visited_order[next_node]==-1)
min_order = min(min_order, FindSCC(next_node));
else if(scc_label[next_node] == -1) //방문은 했지만 아직 scc에 포함되지 않은 노드
min_order = min(min_order, visited_order[next_node]);
}
if(min_order == visited_order[now_node]){
int temp;
while(1){
temp = st.top();
st.pop();
scc_label[temp] = scc_order;
if(temp == now_node)
break;
}
++scc_order;
}
return min_order;
}
void tarjanSCC(){
visited_order = vector<int>(meetings.size()*2, -1);
scc_label = vector<int>(meetings.size()*2, -1);
order =1;
scc_order =1;
for(int i=0; i<visited_order.size(); ++i)
if(visited_order[i] == -1)
FindSCC(i);
}
vector<int> Solve2SAT(){
int meeting_num = meetings.size();
tarjanSCC();
for(int i=0; i<meeting_num*2 ; i+=2)
if(scc_label[i] == scc_label[i+1]) //~i와 i가 같은 scc에 속하는 경우
return vector<int>(); //불가능하다.
vector<int> result( meeting_num*2,-1);
vector<pair<int,int>> sat_order;
for(int i=0; i<meeting_num*2 ; ++i)
sat_order.push_back(make_pair(-scc_label[i], i)); //역순 저장
sort(sat_order.begin(), sat_order.end());
for(int i=0; i<meeting_num*2 ; ++i){
int vertex = sat_order[i].second;
int meeting_idx = vertex/2;
int is_true = (vertex%2 ==0);
if(result[meeting_idx] != -1) //이미 해당 회의(A)가 열릴지 결정된 경우
continue;
result[meeting_idx] = !is_true; //A가 먼저 방문 -> A는 거짓
} //!A가 먼저 방문 -> A는 참
return result;
}
|
cs |
만약 i번째 회의의 변수 값 i와 ~i가 같은 SCC에 속한다면 같은 bool 값을 가져야 하므로 해당 SAT problem은 해결할 수 없습니다.
따라서 이런 경우 불가능을 출력해 줍시다.
사실 여기까지 풀이로 [백준] 2 - SAT - 3 (11280) 문제를 동일하게 해결 가능합니다.
하지만 저희는 각 정점이 어떤 값을 가져야 하는지(= 어떤 회의가 진행되는지)를 구해야 합니다.
본인의 풀이에는 SCC알고리즘 중에서 타잔 알고리즘을 사용했으나 어떤 알고리즘으로 SCC를 구현해도 상관없습니다.
단, 타잔 알고리즘은 스패닝 트리의 역순으로 SCC가 구성되므로 하위 SCC일수록 scc_label의 값이 작습니다.
따라서 진입 차수(indegree)가 0인 SCC부터 참과 거짓 값을 선택하기 위해 scc_label 값의 역순으로 정렬해줍시다.
이제 정렬된 순서대로 해당 회의의 진행 여부를 결정해줍시다.
위에서 설명했듯이 답을 가지는 2-SAT 문제는 특정 SCC와 정확히 대칭되는 SCC가 존재합니다.
따라서 해당 정점을 처음 방문했을 때 거짓으로 설정해주면 대칭되는 SCC들의 정점들은 자동으로 참으로 설정됩니다.
따라서 아래와 같은 경우가 발생하진 않습니다.
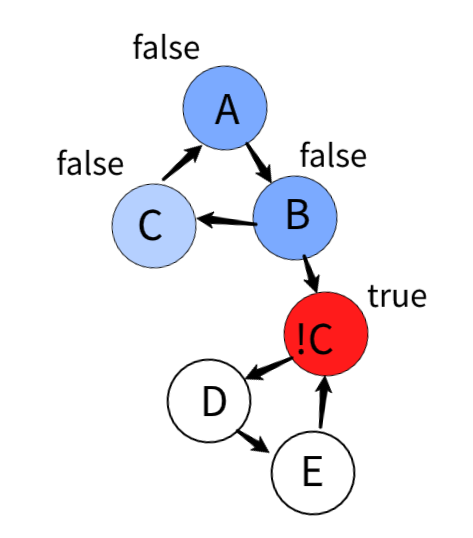
A->B->C가 순서대로 처음 방문되어 false로 설정되어 !A, !B, !C의 값들은 자동으로 true로 설정됩니다.
이때 !C는 이미 값이 결정되었고 D를 방문하면 D는false로 설정이 됩니다.
하지만 명제에 의해 참 -> 거짓은 불가능합니다.
정답이 존재하는 SCC는 이처럼 비대칭의 경우가 발생하지 않으므로 먼저 방문한 변수는 false로 설정해줍시다.
이와 같은 문제로 [백준] 2 - SAT - 4(11281) 도 해결해봅시다.
참고 서적: 알고리즘 문제 해결 전략(구종만 저)
코드
'알고리즘 공부 > 알고리즘 기법' 카테고리의 다른 글
| Trie (Prefix Tree) 구현 문제와 함께 이해하기 (C++) (0) | 2023.07.10 |
|---|---|
| [네트워크 유량] Network Flow(최대 유량, 최소 컷) 알고리즘 (0) | 2021.05.30 |
| [절단선과 절단점] Articulation point, Bridge (Cut vertex, cut edge) (0) | 2021.03.14 |
| [임계 경로 알고리즘] Critical Path Method (백준-1948 해설) (0) | 2021.03.09 |
| [Union-Find] 유니온-파인드, 분리 집합 (백준 1717 - 집합의 표현 해설) (1) | 2021.02.28 |