
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://www.acmicpc.net/problem/11266
11266번: 단절점
첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B
www.acmicpc.net
풀이
solved.ac 난이도: Platium 5
DFS를 응용하여 해결할 수 있는 문제들 중에 하나인 절단점/단절점(Articulation point / Cut vertex)에 대한 문제이다.
절단점(Articulation point / Cut vertex)
절단점이란 무향 그래프에서 해당 점과 인접한 간선들을 모두 지웠을 때 그래프가 두 개 이상의 컴포넌트(서브 그래프)로 나뉘는 정점을 의미한다. 정점들을 절단점인지 확인하는 절차는 DFS로 구현할 수 있다.
정점 u의 자식 노드를 루트로 하는 서브 트리가 u의 조상 중 하나와 연결되어있다면 u는 절단 점이 될 수 없다.
다음과 같은 무향 그래프를 생각해보자.

루트 r에서 DFS형식으로 u를 먼저 방문한 후 u가 절단점인지를 확인하고 싶다면
u의 자식의 서브 트리가 u의 조상인 r과 연결돼있지 않는다면 u는 r과 v의 서브 트리를 둘로 나누는 절단점이 될 수 있다.
하지만 위와 같은 그래프에서는 v의 서브 트리에 r과의 연결된 간선이 있기 때문에 u는 절단 점이 될 수 없다.
그렇다면 정점의 자식의 서브 트리가 조상과 연결되어 있는지를 어떻게 확인할 수 있을까?
이를 구현하기 위해 DFS로 방문한 순서를 저장하는 visited_order []를 사용한다.
해당 정점을 DFS로 방문한 순서를 visited_order에 저장하고,
해당 정점에서 갈 수 있는 가장 낮은(가장 순서가 빠른) visited_order를 반환하자.
만약 자식의 서브 트리가 조상과 연결되어 있다면 해당 정점보다 더 낮은 visited_order를 반환할 것이고 이는 서브 트리의 정점 중에서 조상 정점과 간선으로 연결된 것이 있다는 의미이다.
이를 구현한 코드를 살펴보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
vector<vector<int>> adj;
vector<int> visited_order;
vector<bool> is_cut_vertex;
int order =0, cut_cnt=0;
int FindCutVertex(int now_idx, bool is_root){
visited_order[now_idx] = ++order;
int min_order = visited_order[now_idx];
int subtree_min_order,next_idx, children =0;
for(int i=0; i<adj[now_idx].size() ; ++i){
next_idx = adj[now_idx][i];
if(visited_order[next_idx] == -1){
++children;
subtree_min_order = FindCutVertex(next_idx, false);
if(!is_root && subtree_min_order >= visited_order[now_idx] && !is_cut_vertex[now_idx]){
is_cut_vertex[now_idx] = true; //next_idx의 서브 트리와 연결을 끊을 수 있다
cut_cnt++;
}
min_order = min(min_order, subtree_min_order);
}else{
min_order = min(min_order, visited_order[next_idx]);
}
}
if(is_root && !is_cut_vertex[now_idx]){
is_cut_vertex[now_idx] = (children >=2);
if(is_cut_vertex[now_idx])
++cut_cnt;
}
return min_order;
}
|
cs |
int FindCutVertex(int now_idx, bool is_root) 함수는
방문한 정점 now_idx의 방문 순서를 visited_order[now_idx]에 저장하고
now_idx에서 접근할 수 있는 가장 작은 visited_order를 찾아 min_order에 저장한다.
이를 위해 자신과 연결된 노드들의 방문 여부를 확인한 후 재귀 호출한다.
방문한 노드가 아니라면 DFS 스패닝 트리에서는 now_idx의 자식 노드로서 방문을 하게 된다.
자식 노드(next_idx)를 재귀 호출하여 반환받은 값, 즉 자식 노드의 서브 트리에서 접근 가능한 가장 작은 visited_order(subtree_min_order라고 하자.)
을 자신의 방문 순서 visited_order[now_idx]와 비교하여 만약 subtree_min_order가 같거나 크다면
subtree_min_order >= visited_order[now_idx]
서브 트리에서는 now_idx의 상위 노드와 연결된 노드가 없다는 의미이다.
따라서 now_idx는 해당 서브 트리 컴포넌트와 자신의 조상들의 컴포넌트를 둘로 나눌 수 있는 절단점이 될 수 있다.
만약 자신과 연결된 노드들 중 이미 방문한 노드가 있다면 해당 노드는 자신의 상위 노드일 수밖에 없다.
(상위 노드들을 방문한 후에 자식 노드를 DFS로 방문해 나가기 때문에)
따라서 이미 방문한 노드라면 해당 노드의 방문 순서와 min_order를 바로 비교해주자.
min_order = min(min_order, visited_order[next_idx])
예를 들어 다음과 같은 그래프를 맨 위의 노드부터 방문한다면 오른쪽과 방문 순서를 갖는다.
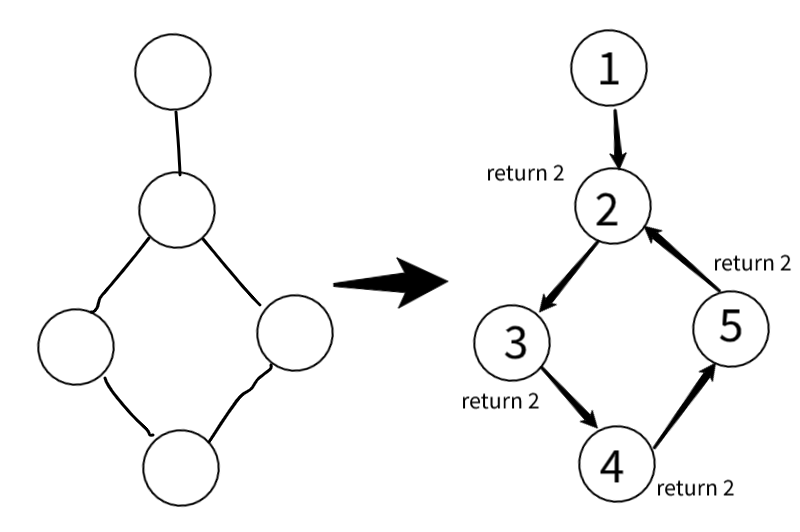
1->2->3->4->5 순서대로 방문하다가 방문 순서 5번 노드는 방문 순서 2번과 연결되어 있다.
이미 방문한 노드의 경우 해당 노드의 방문 순서(visited_order)를 그대로 반환하기 때문에 결국 5,4,3, 모두 2를 반환한다.
방문 순서 2번 노드에서는 subtree에서 연결된 가장 작은 visited_order가 2 이기 때문에
subtree_min_order == visited_order[now_idx]으로 절단점이 된다.
이제 최종적으로 root를 처리해야 한다.
root노드의 경우 연결된 노드가 없거나 자식 노드가 1개라면 루트 노드와 인접 간선을 소거해도 컴포넌트가 두 개 이상으로 나뉘지 않는다.
따라서 root노드가 절단점이 되기 위해서는 자식 노드가 2개 이상이어야 한다.
이를 위해 is_root가 true인 경우 children 변수로 자식 노드의 개수를 세어 반영해주자.
+ 특히 무향 그래프에서 이러한 절단점을 포함하지 않는 서브 그래프를 이중 결합 컴포넌트(Biconnected component)라고한다.
코드
'알고리즘 공부 > 백준' 카테고리의 다른 글
| [백준] No.2150 - Strongly Connected Component (C++, 강결합 컴포넌트, 타잔 알고리즘) (2) | 2021.04.06 |
|---|---|
| [백준] No.11400 - 단절선 (C++, Bridge) (0) | 2021.03.14 |
| [백준] No.18250 - 철도 여행 (C++, 오일러 경로) (0) | 2021.03.13 |
| [백준] No.3665 - 최종 순위 (C++, 위상 정렬) (0) | 2021.03.08 |
| [백준] No.2637 - 장난감 조립 (C++) (0) | 2021.03.08 |