
Go, Vantage point
가까운 곳을 걷지 않고 서는 먼 곳을 갈 수 없다.
Github | https://github.com/overnew/
Blog | https://everenew.tistory.com/
티스토리 뷰
문제
https://www.acmicpc.net/problem/9466
9466번: 텀 프로젝트
이번 가을학기에 '문제 해결' 강의를 신청한 학생들은 텀 프로젝트를 수행해야 한다. 프로젝트 팀원 수에는 제한이 없다. 심지어 모든 학생들이 동일한 팀의 팀원인 경우와 같이 한 팀만 있을
www.acmicpc.net
풀이
solved.ac 난이도: Gold 4
조금 특이한 DFS문제였다.
해당 문제에서 팀이 결성되기 위해서는 서로 선택한 학생들끼리의 사이클이 만들어져야 한다.
이 사이클은 자기 자신을 선택하는 것도 인정한다.
예를 들어 아래와 같은 입력에서 선택 관계를 그려보자.
학생 번호: 1, 2, 3, 4, 5
선택 번호 3, 4, 4, 5, 3
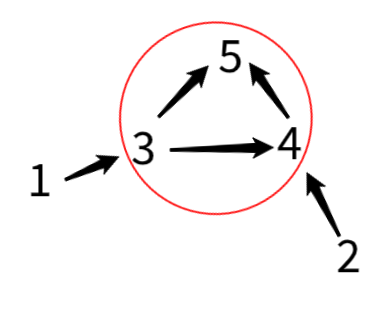
이때 사이클을 구성하는 것은 3->4->5(->3)이다.
사이클을 구성하는 학생들의 수를 찾기 위해 아래와 같은 DFS함수를 작성하였다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
int choice_partner[100001];
bool visited[100001];
int cnt;
pair<int,int> PartnerDFS(int idx,int depth){
if(visited[idx])
return make_pair(idx,depth);
visited[idx] =true;
pair<int,int> ret = PartnerDFS(choice_partner[idx], depth+1);
if(ret.first == idx)
cnt -= ret.second - depth; //팀원의 수
return ret;
}
|
cs |
모든 학생 번호(idx)에 대하여 PartnerDFS(int idx,int depth)를 호출하여
방문한 idx는 visited 표시를 해주고 자신의 idx를 반환해주자.
만약 방문하지 않았다면 선택한 학생과 깊이(depth) +1로 재귀 호출해준다.
위의 예제 입력에서는 PartnerDFS(1, 1)를 실행 시, 아래의 순서대로 호출이 진행된다.
1(depth: 1) -> 3(depth: 2) -> 4(depth: 3) -> 5(depth: 4) -> 3(depth: 5)
마지막인 3번은 이미 방문했으므로 자신의 depth(5)와 자신(idx: 3)을 반환한다.
1(return 3,5) <- 3(return 3,5) <- 4(return 3,5) <- 5(return 3,5) <- 3(return 3,5)
이때 3번에서 자신과 같은 idx를 반환받았으므로 사이클이 성립됐음을 확인할 수 있다.
사이클에 포함된 학생수(= 팀원의 수)는 재방문된 3의 depth(5)와 3의 depth(2)를 빼주어 구할 수 있다.
1번은 3번이 return 되어 자신과 같지 않으므로 사이클에 포함되지 않는다.
2번의 경우 4번을 DFS로 호출하지만 이미 방문되어 4번이 반환된다.
2번 또한 자신과 같은 idx를 반환받지 않았으므로 사이클을 만들지 못한다.
자기 자신을 선택하는 경우를 생각해보자.
만약 6번이 자기 자신을 선택했다면
PartnerDFS(6, 1)을 호출하여 6번의 visited 표시한 후, 자기 자신(idx:6)을 재귀 호출할 것이다.
6은 이미 방문되었으므로 6이 다시 반환되어 자신과 같은 idx를 반환받았으므로 사이클이 성립한다.
문제에서는 팀에 속하지 않는 학생들의 수를 구하고 싶으므로
전체 학생수(cnt)에서 사이클로 구한 팀들의 인원수를 모두 빼주어 구할 수 있다.
코드
'알고리즘 공부 > 백준' 카테고리의 다른 글
| [백준] No.2637 - 장난감 조립 (C++) (0) | 2021.03.08 |
|---|---|
| [백준] No.2848 - 알고스팟어 (C++, 위상 정렬) (0) | 2021.03.07 |
| [백준] No.13306 - 트리 (C++, 오프라인 알고리즘) (0) | 2021.03.03 |
| [백준] No.17619 - 개구리 점프 (C++) (0) | 2021.03.01 |
| [백준] No.4195 - 친구 네트워크 (C++, 분리 집합) (1) | 2021.03.01 |